教養番組「知の回廊」57「近道のための数学～アルゴリズムを考える～」

私達の社会の中には、さまざまな数学が応用されています。
その中で、『アルゴリズム』という言葉を、聞いたことはないでしょうか？ 
これは私たちにとって非常に身近なもので、ある物事の問題を解き、目的を果たすための『手順』や『流れ』のことなのです。
コンピュータの世界では、プログラムを作る時の土台となる概念で、私たちが普段利用している、電車の乗り換え検索や、カーナビゲーションからの情報。
または旅客機の離陸経路や、通信・物流・遺伝子情報学など、幅広い分野の中で、アルゴリズムが活躍しています。
今回は、このアルゴリズムという、数学の道具を用いて、様々な分野を開拓してゆく、情報工学の世界をご案内しましょう。

アルゴリズムという言葉は、最近新聞やテレビ等でも使われるようになりました。
もともとはアルファ=リスミーという、人の名前なのですが、今では『手順』や『手続き』を意味する言葉となっています。
私たちの身の回りにあるアルゴリズムの簡単な例として、料理のレシピがあります。
レシピの通り、材料を切ったり煮たり焼いたりすれば、誰でも達人の味の料理が作れる。これがアルゴリズムの力です。
また、このような料理の手順、これがアルゴリズムそのものなのです。
皆さんが家に帰るとき、本屋に寄って、薬屋に寄って、最後にスーパーに寄って帰ろうと、そんな風に考えていたら、それは皆さんが今日の自分の行動のアルゴリズムを作っていることに他なりません。
実はアルゴリズムは皆さんの身の回りにあふれています。洗濯機を回せば、洗って、すすいで、絞る、という手順が組み込まれています。銀行にいけば、カードを入れて暗証番号を打ち込むという手順が組み込まれています。
今日は、最も短い道、最短経路を探す、と言う問題に着目して、身の回りにあるアルゴリズムの世界へ皆さんをご案内しましょう。

アルゴリズムは、幅広い分野で用いられていますが、その代表的な例が、カーナビゲーション・システムなどで用いられる、最短経路を求める方法で、どの経路が最も早いか、または最小コストで移動できるか、など、近道を求めるために、アルゴリズムが用いられています。

たとえば、このような碁盤目の道を辿って行くとしましょう。
もし、左下から右上までの道を移動する場合、すべての経路を辿っていくとすれば、19本×19本の碁盤目の場合、その数は、なんと90億通りもの経路があるのです。
コンピュータを用いて、最も早く目的地に到達するための経路を、1本ずつ探していくと、1秒間に100万本の経路を調べることができるコンピュータを使ったとしても、すべてを調べるには2時間以上もかかってしまいます。
これでは、カーナビゲーションなどの検索には、とても実用的でありません。

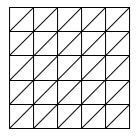
また、碁盤目に対角線をつけて経路を増やせば、8兆もの経路となり、さらに時間がかかってしまいます。
つまり、カーナビゲーションの仕組みは、全ての経路を1本ずつ調べているわけではないのです。
では、どのような仕組みで最短経路を求めているかというと、ここにアルゴリズムが用いられているのです。
専門的には、動的計画法やダイクストラ法という、アルゴリズムの計算式を用いて、 

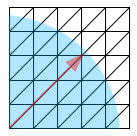
たとえばこのように、出発点から波紋が広がっていくようなイメージで、同時にすべての地点への最短経路を求めながら、目的地まで、最も短時間で到達できるルートを計算し、結果を表示しているのです。
このように、アルゴリズムの手法を用いれば、さらに複雑な経路でも、一瞬で答えを見つけ出すことができます。

最短経路を求めるアルゴリズムの手法は、カーナビゲーションの道案内だけでなく、鉄道網の路線検索にも使われています。
皆さんも外出される時は、インターネットで電車の乗り継ぎや案内や運賃などを調べたりしていないでしょうか？ 
これらの検索システムの中にも、最短経路を求めるアルゴリズムが潜んでいます。
路線検索の代表的な例として、『駅すぱあと』の開発で有名な、株式会社ヴァル研究所を訪れてみました。 (内容は番組をご覧下さい)

最短経路を求めるアルゴリズムは、航空機の分野でも応用されています。
旅客機の飛行には、コストの面から、最も燃料消費の少ない操縦経路が求められます。

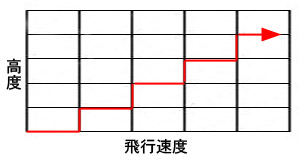
旅客機が離陸し、一定の巡航速度と所定の高度に達するまでの経路をグラフで示すと、このようになります。
航空機は、高度を上げているときは速度が伸びず、その逆に、速度を出しているときは高度が上がらないという、相反する二つの特性を持っています。
この特性を両立させながら、できるだけ燃料の消費を抑え、離陸してから、所定の高度と巡航速度に到達しなければなりません。
先に速度を出してから高度を上げるか、または、高度を上げてから速度を出すか、さまざまな離陸経路を選択することによって、その燃料消費量に違いが出てくるのです。
この問題に対しても、最短経路を求めるアルゴリズムが応用されています。

航空技術におけるアルゴリズムは、離陸経路を設定するだけではありません。
たとえば皆さんが旅客機を利用する場合、搭乗口から旅客機に乗り、離陸していきますが、この時の、機体が滑走路まで進む経路についても、最短経路を求めるアルゴリズムが潜んでいるのです。
滑走路までの経路の設定は、早いことだけでなく、安全性を考慮する必要があり、そのような研究をされておられる方々もいらっしゃいます。(電子航法研究所の取材内容は番組をご覧下さい)

もっと身近な例をご紹介しましょう。
ベースギターで単旋律を演奏するとき、どのように弦を押さえるか、そんな運指の方法について考えてみましょう。

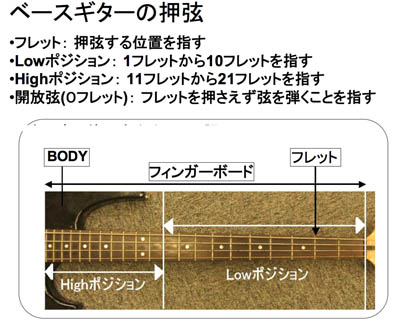
ベースギターには4本の弦があり、フレットと呼ばれる21箇所の押さえる場所があります。
この押さえる場所を変えれば、違う弦で同じ音を出す事ができます。
ですから、単旋律を演奏する際に、どの弦で音を出すかによって押さえるポジションが変わり、演奏のし易さも変わります。
演奏しやすい運指を考える問題、これにも最短経路を求めるアルゴリズムを使うことができます。
私達は、ある運指から違う運指に移動するとき、それがどのくらい大変かを、アンケートを元に数値化しました、 
そして、演奏する旋律の各音に対し可能な運指をすべてリストアップします。

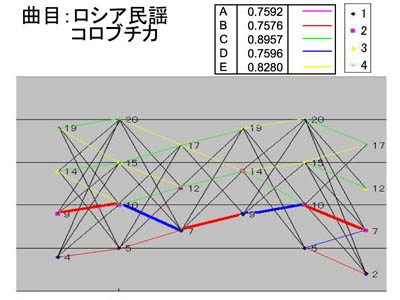
この、可能な運指を駅と考え、運指間の移動の大変さを、駅間の距離と考えます。
すると、曲の始めの音から最後の音までの経路のうち、最も短いものを探せば、これが演奏しやすい運指になると考えたのです。
これは、ベースギターを学んでいる初心者にとって、便利な情報になるだろうと考えています。
同様なことは、他の楽器でももちろん可能です。
では、フルートの運指について研究された方のお話も伺ってみましょう。(フルートの運指最適化は番組をご覧下さい)

近年大きな発展をとげた分野に遺伝子工学、生体情報学があります。
これらの学問は、新薬の開発や病気の治療に力を発揮しますが、実は私たちの身の回りでも活用されつつあります。
皆さんがスーパーや魚屋で買う魚、鮮魚や缶詰はどこで取れたものでしょう。
本当に表示された海でとれたものでしょうか？。
最近このような問題がクローズアップされています。
そこで、店頭にならんでいる魚の原産地を特定するために、その遺伝子を解析するという技術が開発されつつあります。
つまり、店頭にならんでいる魚と、日本海の魚、インド洋の魚をくらべて、どれが近いかを調べるわけです。
ここでは、蛋白質解析の例をとって、生体情報学において最短経路のアルゴリズムが使われていることをお話ししましょう。

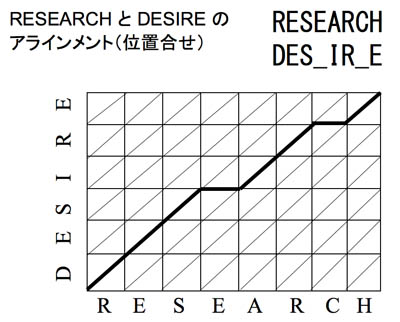
例えば、RESEARCHという、アミノ酸が8つ繋がった蛋白質と、DESIREという、アミノ酸が6つつながった蛋白質がどのくらい近いか考えて見ましょう。
この2つの蛋白質は、並びも長さも違います。
この2つの蛋白質は、アミノ酸の欠失挿入が起こったり、置き換えが起こって変化したものと考えられます。
このように、2つの蛋白質を位置を合わせて並べることを、アラインメント（位置合せ）と言います。
例えばこのアラインメント以外にも様々なアラインメントがありえます。
2つのアミノ酸配列を縦と横に並べた図を考えると、実はこのようなアラインメントは、この図で左下から右上まで辿る経路になっていることが分ります。

この図を鉄道網と考え、それぞれのアミノ酸の置き換わりにくさや、欠失挿入の置きやすさを駅間の距離と考えると、左下から右上までの経路のうち最も近い経路をさがせば、その距離が2つの蛋白質の近さと考えることができます。
このように、蛋白質の近さを測る問題にも、最短経路を求めるアルゴリズムが使われているのです。

社会において、私たちが解かなければならない問題は、その時代や分野によって、日々変化していきます。しかし数学は、常にそれらを解く基礎技術であり、普遍的な『道具』なのです。
社会が変わっても、また分野が違っても、それが変わることはありません。
情報工学というと、一人でコンピュータに向かって研究するといったイメージを持たれがちですが、実際は、外に出て、様々な人と対話し、アルゴリズムなどの基礎的な道具を駆使して、身近な問題を解いてゆくという、社会に向かって開かれた学問なのです。